
| myArmoury.com is now completely member-supported. Please contribute to our efforts with a donation. Your donations will go towards updating our site, modernizing it, and keeping it viable long-term.
Last 10 Donors: Piotr H. Feret, Graham Shearlaw, Anonymous, Daniel Sullivan, Chad Arnow, Jonathan Dean, M. Oroszlany, Sam Arwas, Barry C. Hutchins, Dan Kary (View All Donors) |
| Author |
Message |
|
Mark Lewis
|
 Posted: Mon 14 Nov, 2016 10:27 pm Post subject: Experimenting with Peter Johnsson's geometric theories Posted: Mon 14 Nov, 2016 10:27 pm Post subject: Experimenting with Peter Johnsson's geometric theories |
 |
|
I was immediately intrigued by Peter Johnsson's geometric theories of sword design, and now that I have finally (long story) received my copy of The Sword - Form and Thought and familiarized myself with at least the basic principles, I thought I would try my hand at analyzing the geometry of a few swords myself.
Out of necessity I have to work from photographs, not proper scale drawings, so optical distortions are a concern. This can be avoided to some extent by limiting the candidates for analysis to swords with photos that show little distortion in comparison to available measurements - most photos don't make the grade. Still, any apparent geometric relationships should be considered approximate at best and "for entertainment purposes only".
My initial results have still been very encouraging - most of my first round of attempted analyses seemed to quickly reveal underlying ratios and relationships, including two swords with nearly identical proportions (which I hadn't anticipated beforehand).
If others want to or already have been working on geometrical analyses, maybe this thread can be used to collect a variety of examples for discussion. If anyone has suggestions for swords they would like to see analyzed I'm willing to give it a try, time permitting (and given adequate photos and measurements). I think it would be particularly interesting to collect examples of swords that just seem to naturally stand out as being intuitively well proportioned, as well as the opposite swords that just seem oddly proportioned.
My first successful(?) attempts at analysis are shown below - it's a pretty random assortment chosen in large part based on which photos I felt were sufficiently free from distortion. I've combined separate files to create this composite diagram - the swords may not be perfectly to scale from one to the next, but should be quite close. My comments on each sword follow below.

Starting on the left, the first two swords are from Utrecht and Veste Coburg respectively, the latter bears the inscription SININIS. These two seem to have virtually identical proportions, the guide lines of one were literally a cut-and-paste job from the other. The hilt is one seventh of the total length - the proportions are constructed with a series of 7 adjacent circles, with the cross aligned within the first circle. The diameter of the basic circle provides the width of the cross, thus the hilt dimensions form a perfect square.
Next from left is a sword in Brussels with a very dramatic profile. The underlying geometry appears to be more complex - constructing the total length with 11 interlocking circles, the cross aligns with the vesica of the first two, forming a type II structure in Johnsson's terminology. The basic circle traces the upper arc of the wide type A pommel, the lower arc is symmetrical. The cross is roughly twice as wide as the hilt is tall, and five times the width of the blade.
Next is one from Plock in Poland, with an inscription possibly resembling LEUTLRIT. The sword is short with a hilt to blade ratio of 1:5. The cross aligns with the diameter of the basic (large) circle - Johnsson's type I structure. An inscribed square aligns with the base of the very large pommel, but I couldn't find any geometric construction for the width of the cross...
The proportions of the Imperial Sword in Vienna are elegantly simple. It follows a type I structure with measurements very similar to the previous sword (just try overlaying them). Now the inscribed square perfectly provides the width of the cross, which forms a ratio of 7:5 with the height of the hilt. The long type XI blade forms a 7:1 ratio with the hilt.
Last but not least... Oakeshott mentions the unique proportions of this sword from the Musée de l'Armée in Records of the Medieval Sword; he also describes it as "enormous", which it isn't. The ratio of hilt to total length is 1:7 like the first two swords, but with the cross placed outside of the first circle instead of inside. The type G pommel is two fifths the diameter of the basic circle. The width and height (measured from above the cross) of the hilt are in the ratio of 5:8 (measurable with 5 x 8 pommel radii) which is very close to the Golden Ratio of φ = 1.618... The diagram shows an approximate construction of the Golden Ratio using a Fibonnaci Spiral. The gently curving cross follows the arc of a great circle passing through the tip of the blade. The second basic circle also seems to indicate the width of the very broad blade where it meets the cross.
|
|
   |
 |
J. Helm

Location: WA, USA Joined: 17 Jun 2011
Posts: 33
|
 Posted: Tue 15 Nov, 2016 12:54 pm Post subject: Posted: Tue 15 Nov, 2016 12:54 pm Post subject: |
 |
|
You may want to check out this other discussion thread which got some feedback from Vincent Le Chevalier who apparently worked on the graphs for the book, and Peter also chimed in.
Sword Form and Thought Chart creations
Edit: I'm not familiar with the book myself, and this may be a slightly different topic by the looks of your graphs (proportions/ratios), but I'm just pointing it out.
|
|
   |
 |
|
Mark Lewis
|
 Posted: Wed 16 Nov, 2016 10:32 am Post subject: Posted: Wed 16 Nov, 2016 10:32 am Post subject: |
 |
|
Thanks for the reminder! I had seen that thread but forgotten about it. The graphs I am interested in different than the ones discussed there however - ratios between various measurements versus weight distributions. I would be happy to receive any feedback...
I have prepared two more diagrams that revealed some interesting and unexpected similarities. The first sword is the Soborg type XI. I identified the basic ratio and geometric structure myself, with the cross placed precisely at the first vesica of 10 interlocking circles... then I cheated and copied the rest of Johnsson's construction. I was able to duplicate all of the geometry working from the available photo. The original illustration and my version are shown below.
 
A sword in Zurich from Lake Morat is at first glance very different - type Xa (according to Marko Aleksic), quite short, type N pommel... however it has the same underlying ratio and structure, and I found that the geometric principles of the hilt are essentially the same with only minor adjustments needed for the different pommel and broader blade.

In profile, the pommel of the Morat sword forms a semi-circle two fifths of the diameter of the basic (large) circle used to define the primary ratio. A series of three or five circles defines various hilt proportions, the small circles of the Soborg sword are also approximately two fifths of its basic circle. The two flanking basic circles identify the width of the tang and blade. The underlying sequence of circles for the Morat sword is positioned higher than for the other, with the first circle centered at the upper edge of the pommel - the flanking circles are then proportionally closer together, and various intersection points correctly predict the broader blade and tang of the Morat sword.

The overall construction yields hilts with a height to width ratio of approximately 6:7, the width of the cross and the length of the grip are very close to the golden ratio. The Soborg sword is overall about 20% larger than the Morat sword - a ratio of 6:5.
Last edited by Mark Lewis on Thu 17 Nov, 2016 5:28 am; edited 1 time in total
|
|
   |
 |
|
Niels Just Rasmussen
|
 Posted: Thu 17 Nov, 2016 4:34 am Post subject: Posted: Thu 17 Nov, 2016 4:34 am Post subject: |
 |
|
Great work Mark!
Now it's just the big question - what does it all mean?
Many of the swords definitely seems to be constructed from a geometric standpoint, where different ratios probably symbolizes different things (aesthetics, philosophy, science and religion) all coming together.
Not really surprising to find this on swords, when you also see impressive geometric layouts in gothic cathedrals. The ordering of the heavens (God) being reflected below (Man) so you build an ordered earthly "City of God" (Christian community) as a mirror image of the heavenly City of God (New/Heavenly Jerusalem of St. Augustin & Book of Ezekiel).
The golden division seems to be both genetically linked to our sense of aesthetic beauty and also in a religious sense of being a divine proportion fit for religious buildings. [This is old graeco-roman thinking taken over by the Christian Church].
When you find the golden division on an inscribed christian sword like the one from Søborg it is likely a synthesis of the aesthetic and the religious at work. For an medieval mind the one was probably unthinkable without the other.
The big question is if there was some kind of "code" for the particular choice of geometry between these swords?! Different geometries could highlight different religious aspects interpreted in a Christian way.
|
|
  |
 |
|
Mark Lewis
|
 Posted: Thu 17 Nov, 2016 7:17 pm Post subject: Posted: Thu 17 Nov, 2016 7:17 pm Post subject: |
 |
|
| Niels Just Rasmussen wrote: | Great work Mark!
Now it's just the big question - what does it all mean?
Many of the swords definitely seems to be constructed from a geometric standpoint, where different ratios probably symbolizes different things (aesthetics, philosophy, science and religion) all coming together. |
Thanks Niels! 
Almost any number can have numerological significance... Three for the Trinity, four for the evangelists, five for the wounds of Christ, six for the days of creation... 
Here is another one that I know you will recognize - the very large XI from Esrum Mollegard. I don't really like the proportions of this one actually... it shares the basic proportions of the Reichsschwert, but the simplicity and elegance of the hilt are lost. Both have a hilt to blade ratio of 1:7, enhancing the impression of great length (several other large XI's that I have checked still have a ratio of 1:6).

I was able to locate all the dimensions of the hilt using circles based on the curvature of the pommel - but the result is messy, as you can see. Maybe there is a more elegant construction...
The basic sequence of circles defines the lower arc of the pommel and correspond with the width of the inscribed square, which aligns with the base of the pommel. An offset pair of the same size defines the upper arc of the pommel and the upper edge of the cross.
 
The width of the cross and blade are defined from another overlapping sequence of four circles. Inscribed equilateral triangles identified the center point of the outer circles, and also define the width of the blade at intersection with the inscribed square.

The width of the cross and height of the hilt form another golden ratio. The grid lines based on the dimensions of the blue circles define another golden rectangle which encloses the pommel (though the pommel itself is narrower).
 
|
|
   |
 |
|
Peter Johnsson
Industry Professional
|
 Posted: Fri 18 Nov, 2016 2:41 pm Post subject: Posted: Fri 18 Nov, 2016 2:41 pm Post subject: |
 |
|
Mark, It is great to see what you have done here. It is like the work I have invested in analysing the proportions of swords and possible underlying geometric structures for their design takes on a life of its own.
It is especially exiting how you have found similar structures present in the swords you have looked at, that I already have found to be defining other swords. I can guess at some possible geometric "strategies" that would explain some elements that are now a bit uncertain or overly complex in your analysis. The eight pointed star with a circle is a favourite "trick of the trade" in gothic architectural design that also occurs frequent in defining the proportions of swords. I suspect that guard widths on some of the swords in this thread follow this principle.
Most of the swords you show seem to fit type I structures, with the guard placed in the middle of the first circle. You do not draw this large circle out in all of the structures, however. I think that if you did that and used geometric cuts of that circle (and/or its square) you would find simple (simpler?) solutions for the details of the hilts. especially the width of the blades might be modular functions of the diameter of the large circle, or a result of simple geometric cuts of the same.
I have found it to be a common feature that a square constructed from the width of the guard is involved in the definition of the proportions of the pommel on many brazil nut swords that are based on type I structures.
Another very common strategy is to inscribe two octagons in the two small circles of the first large circle. The distance between the sides of the octagons often define the height of the guard. (While the width of the guard is often a geometric cut or a modular division of the large circle, as mentioned above). The width of the blade is often 1/5 of the diameter of the large circle, or the width of the side of one of the small inscribed octagons.
As you have noted there is often a kind of "communication" or commensurability between the different geometric definitions. A kind of "rhyme and reason" in the choice of numbers.
All of this is mentioned and sometimes covered in detail in the articles I have written for the catalogue of the Solingen exhibition "The Sword - Form & Thought".
You may also find some additional information in the article published in the catalogue for the 2012 exhibit at the Wallace Collection: "The Noble Art of the Sword". In this, I presented geometric analysis of the proportions of three swords in the Wallace Collection.
It must be stressed, however, that photographs are not a reliable basis for analysis of proportions. The parallax effect of camera lenses always changes the proportions of a sword. Sometimes the change can be quite minimal, but often it is severe enough to have an effect on the analysis. All that aside, I think you can get a basic idea from photos such as the ones you have shown in this thread. With a full set of reliable dimensions from the museum (or a first hand documentation has to be made) the indications may be strengthened or refuted.
I am happy to see this hypothesis of mine being tested by others. It is really exiting to see how some "strategies" are common and how some correlations does repeat themselves in many swords.
There are some "rules" to observe when making this kind of analysis.
Before any further analysis can be made, the whole sword must be seen to fit one of the three basic structures: type I with the guard in the middle of the first circle, type II with the guard in the middle of the first vesica, or type III with the first circle defining the full hilt. The point of the blade must rest at the circumference of a circle that is linked to the basic structure.
You might think that you could fit any and all swords in any of these three structures, but that is not the case. Only by following certain modular ratios in their proportions will swords fit one (or in some cases two) of these structures.
An example of a proportion between hilt and blade that may fit two structures is 1:5 for a type I structure of 1:5 that may also fit a type II structure of 3:15. Which one the is the most reasonable depends on the other proportions of the sword (such a size of pommel and width of guard and blade). The design elements can never be too small or too narrow in the geometric structure, or the construction becomes uncertain and complex. There is a matter of scale to be observed when making these constructions. The details must be possible to define with simple geometric constructions with compass and straight edge. If they become too small, they disappear in the uncertainty of the drawing and the thickness of the lines. This is difficult to describe in words but readily recognisable once you try making these constructions by hand yourself.
Another "rule" is that *all* important elements of the design of the sword must be defined by a simple strategies in the same layout, so that all parts are clearly shown in a coherent commensurable way.
There are a few articles about this hypothesis on geometric design of medieval swords on my home page, but it is unfortunately down for the moment. I hope to get it up and running soon.
For those who are curious to learn more I suggest getting a copy of the catalogue: The Sword, Form & Thought. It can (must) be bought directly from the Deutsches Klingenmuseum with payment via wire transfer by bank. We had hoped to make the catalogue available on Amazon, but German bureaucracy put a stop to that.
See below two swords that both comply to type I constructions and make use of inscribed octagons in the small circles as important elements of the design. Another very common strategy seen in both of these swords is the eight pointed star & circle that is used to define guard width.
The blade width in one case is a modular 1/5th of full circle and in the other 1/4th of the first inscribed square.
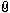 Attachment: 57.92 KB Attachment: 57.92 KB
|
|
   |
 |
|
Mark Lewis
|
 Posted: Sat 19 Nov, 2016 9:24 pm Post subject: Posted: Sat 19 Nov, 2016 9:24 pm Post subject: |
 |
|
Hi Peter,
Thanks for your very detailed response, I was hoping to get your feedback!
Trying to create these diagrams has been very helpful to me for understanding the diagrams in Form and Thought - which I still need to finish reading properly. Already I feel like I have a much better sense of how the geometry is arrived at. I wasn't expecting to see common ratios and structures appearing so quickly, and it was very satisfying to see even just basic elements that could be transferred from one sword to another.
I will definitely try revising my diagrams based on your suggestions - I hadn't tried any constructions beyond circles and squares so far, but I can already see that the inscribed octagons will be useful! The guard/pommel square is another element that I would not likely have thought to try, the diagrams of the Kelvingrove swords are very helpful in demonstrating this. So far, I have cleaned up and (I think) greatly improved my diagram of the Reichsschwert and it seems like it may have a very similar structure.
I'm definitely aware of the limitations of working from photos, so have tried to be very selective and only attempted an analysis of photos that I can compare with at least a basic set of measurements. Even so, I will try to maintain a healthy skepticism of my own diagrams!
For the Reichsschwert I have been working based on photos and illustrations taken from the article "Schwerter des 10. jarhunderts als herrschaftszeichen der Ottonen" by Mechthild Schulze-Dorlamm. I've cleaned up the linework of the type I structure I had drawn previously, and added the octagons to define the hilt, and the square based on the width of the cross. I now suspect the intended ratio between height and width of the hilt in this case is 1:√2 - part of the construction creates a rectangle which is proportional to half of itself, which necessarily implies this ratio. 7:5 which I had suggested previously is a close approximation to the irrational ratio.
 
The blade seems like it may be based on one third the diameter of the basic circle. Stacking 6 circles vertically across the large outer circle creates nice symmetries when combined with various positions of inscribed squares having the diagonal width of the cross. The ratio of the sides to the diagonal of a square is 1:√2, and the overall design naturally creates additional 1:√2 ratios on many scales and orientations.
     

Hope to hear your thoughts on version 2.0!
|
|
   |
 |
|
Mark Moore
|
 Posted: Sun 20 Nov, 2016 5:43 am Post subject: Posted: Sun 20 Nov, 2016 5:43 am Post subject: |
 |
|
  You guys are the ones making all the CROP CIRCLES!!! NOT ALIENS!!! You guys are the ones making all the CROP CIRCLES!!! NOT ALIENS!!!   ......McM ......McM
''Life is like a box of chocolates...'' --- F. Gump
|
|
  |
 |
|
Mark Moore
|
 Posted: Sun 20 Nov, 2016 5:47 am Post subject: Posted: Sun 20 Nov, 2016 5:47 am Post subject: |
 |
|
Sorry about that....it's early, and it's my birthday....I'm allowed one shot where I can take it....  .....McM .....McM
''Life is like a box of chocolates...'' --- F. Gump
|
|
  |
 |
Luka Borscak

|
 Posted: Sun 20 Nov, 2016 7:37 am Post subject: Posted: Sun 20 Nov, 2016 7:37 am Post subject: |
 |
|
Happy birthday! 
|
|
  |
 |
|
Mark Moore
|
 Posted: Sun 20 Nov, 2016 8:18 am Post subject: Posted: Sun 20 Nov, 2016 8:18 am Post subject: |
 |
|
Thanks, Luka! I really didn't mean to interrupt the flow of this topic....just had to....I was beckoned from beyond..  ....McM ....McM
''Life is like a box of chocolates...'' --- F. Gump
|
|
  |
 |
|
Mark Lewis
|
 Posted: Mon 21 Nov, 2016 4:20 am Post subject: Posted: Mon 21 Nov, 2016 4:20 am Post subject: |
 |
|
Happy Birthday Mark. Almost mine too... missed by just a couple days! 
To get back on track, here is another crop circle - much simpler this time! I tried to analyze the type XI from Jamsa, Finland, which has an inscription that is sometimes compared to the Soborg sword (see Swords of the Viking Age).
The proportions seem to follow from the basic circle in a nice simple way - the cross follows the base of a square circumscribing the circle, it's height is defined by the two octagons, and the pommel (which is not perfectly circular) is one third the diameter of the basic circle, which is also close to the width of the blade - difficult to compare because of the edge losses.

An equilateral triangle based on the cross aligns almost with the center of the pommel. I didn't seem to need to use the large circle in any way - in particular the baseline of the pommel does not come from an inscribed square. Maybe a different construction could connect those...
I've compared the construction against as many photos as I had available, to check for inconsistencies... So far, so good. 
|
|
   |
 |
|
Niels Just Rasmussen
|
 Posted: Mon 21 Nov, 2016 10:44 am Post subject: Posted: Mon 21 Nov, 2016 10:44 am Post subject: |
 |
|
| Mark Lewis wrote: | | Niels Just Rasmussen wrote: | Great work Mark!
Now it's just the big question - what does it all mean?
Many of the swords definitely seems to be constructed from a geometric standpoint, where different ratios probably symbolizes different things (aesthetics, philosophy, science and religion) all coming together. |
Thanks Niels! 
Almost any number can have numerological significance... Three for the Trinity, four for the evangelists, five for the wounds of Christ, six for the days of creation... 
Here is another one that I know you will recognize - the very large XI from Esrum Mollegard. I don't really like the proportions of this one actually... it shares the basic proportions of the Reichsschwert, but the simplicity and elegance of the hilt are lost. Both have a hilt to blade ratio of 1:7, enhancing the impression of great length (several other large XI's that I have checked still have a ratio of 1:6).
I was able to locate all the dimensions of the hilt using circles based on the curvature of the pommel - but the result is messy, as you can see. Maybe there is a more elegant construction...
The basic sequence of circles defines the lower arc of the pommel and correspond with the width of the inscribed square, which aligns with the base of the pommel. An offset pair of the same size defines the upper arc of the pommel and the upper edge of the cross.
The width of the cross and blade are defined from another overlapping sequence of four circles. Inscribed equilateral triangles identified the center point of the outer circles, and also define the width of the blade at intersection with the inscribed square.
The width of the cross and height of the hilt form another golden ratio. The grid lines based on the dimensions of the blue circles define another golden rectangle which encloses the pommel (though the pommel itself is narrower).
|
Happy birthday Mark and Mark. Is this a scorpio convention, since I just had my birthday as well 
It's very interesting with the 1:7 point ratio that you compared with the Reichsschwert as most type XI swords have a 1:6 ratio of hilt to blade. Is this a Danish "copy" of a sword associated with the Holy Roman Emperor? A way for the Danish Kings to have their own royal sword as statement to their independence? We don't know the age of the Esrum sword, but apparently the Reichsschwert is from around ~1200.
As the golden rations of pommel & width of the cross and height of the hilt shows clear deliberation, it is interesting that the rest of the sword fails to fit the scheme. It seems the problem lies with the crossguard, which is too wide, because right now with this crossguard the geometry gets overly complex as you showed.
1) As Peter Johnson stated it could be a problem with the picture. It seems the image is taken at an angle. That could account for your failure to get the geometry to fit?
2) Or perhaps an owner found the crossguard to short to be practical, which caused the disruption of the geometry?
Without having seen more of the sword than this image, there is some asymmetry with the crossguard; so one does wonder if it is original, later repair or a total change (from the picture it almost looks like they are hammered out - and we see the Boringholm sword fashion of "outflaring" crossguards later on).
The Søborg sword does have the same kind of shorter simple crossguard as the Reichsschwert; so I would speculate that perhaps the Esrum sword has a later crossguard fashion!?
The sword has to be seen in detail before we can say whether 1) or 2) is correct, or 3) it's just the case of the smith not getting it absolutely right.
|
|
  |
 |
|
Mark Lewis
|
 Posted: Tue 22 Nov, 2016 9:39 pm Post subject: Posted: Tue 22 Nov, 2016 9:39 pm Post subject: |
 |
|
The cross on the Mollegard sword is definitely damaged/skewed/distorted in the photo/etc. so any geometrical design is conjecture at best! Nevertheless, I've tried to clean up my diagram and come up with a better construction.
I couldn't find a direct construction that gives the width of the cross using any inscribed squares, octagons, stars, etc... Forming the golden ratio based on the height of the hilt seems like enough justification on its own for the wide cross? The width also seems to be predicted by creating a triangle that aligns with vertices of the upper octagon and has it's point at the base of the pommel (in line with the inscribed square).
The curvature of the pommel should probably be based on a circle half the diameter of the basic circle. The width of the blade seems to be one third of the basic circle, or equivalently the sidelength of an equilateral triangle placed between the the large circle and the bottom side of the inscribed square.

I found a similar pattern with another type N sword from Warsaw that I wanted to compare to the one posted above (and another in Sword and Thought). Again it's a half-diameter for the pommel, a third for the blade, or the equivalent equilateral triangle construction - which in this case can be drawn directly from the cross, much simpler than the Mollegard sword. Inscribed octagons don't seem to measure out the height of the cross this time. The 2:√3 ratio of the hilt is implied by the rectangle which inscribes an equilateral triangle (which also creates 30º/60º/90º triangles - well known to geometry students!).
|
|
   |
 |
|
Peter Johnsson
Industry Professional
|
 Posted: Wed 23 Nov, 2016 3:26 am Post subject: Posted: Wed 23 Nov, 2016 3:26 am Post subject: |
 |
|
Mark, I follow this with interest.
There are a number of things I would like to comment on, but I am unfortunately very short of time.
The sword from Warsaw is interesting. As you noted, the inscribed octagon will not give the solution to the guard height. However, I think an inscribed hexagon will. Two inscribed circles in one circle will give you the height of the side of a hexagon that is inscribed in the same circle. Such an inscribed hexagon would give you both the width of the pommel at the same time as it would give you the height of the guard. Try it. I think it would work.
I will return with comments both on the Saint Maurice of Wienna and the Mollegard sword. I hope to get time some evening later this week to work out some drawings showing what I think.
I have a construction of the Wienna St Maurice that is based on actual measurements of the original. I am not at liberty to share the measurements, but the "ghost image" that I have been able to construct will show quite clearly how much of a discrepancy there can be between photos or non-specified drawings and true-to-proportion renderings.
-I will return!
:-)
|
|
   |
 |
|
Peter Johnsson
Industry Professional
|
 Posted: Wed 23 Nov, 2016 10:27 am Post subject: Posted: Wed 23 Nov, 2016 10:27 am Post subject: |
 |
|
See below the use of an inscribed hexagon to define the guard height and the pommel diameter.
 Attachment: 142.38 KB Attachment: 142.38 KB
[ Download ]
|
|
   |
 |
|
Mark Lewis
|
 Posted: Wed 23 Nov, 2016 1:05 pm Post subject: Posted: Wed 23 Nov, 2016 1:05 pm Post subject: |
 |
|
Thanks Peter, the hexagon does seem to fit perfectly! 
Looking forward to hearing your additional comments...
|
|
   |
 |
|
Peter Johnsson
Industry Professional
|
 Posted: Thu 24 Nov, 2016 2:21 am Post subject: Posted: Thu 24 Nov, 2016 2:21 am Post subject: |
 |
|
| Mark Lewis wrote: | Thanks Peter, the hexagon does seem to fit perfectly! 
Looking forward to hearing your additional comments... |
It is indeed tempting, but remember: we cannot really know until we have reliable data on dimensions and a good reproduction of the outline of the sword. I have seen very nice preliminary geometries crash and burn spectacularly when I later had the opportunity to document and analyse the original sword.
-Small details and flaws in the image matters!
This is only very preliminary results that suggest a possible solution.
|
|
   |
 |
|
Mark Lewis
|
 Posted: Thu 24 Nov, 2016 4:18 am Post subject: Posted: Thu 24 Nov, 2016 4:18 am Post subject: |
 |
|
| Peter Johnsson wrote: | | This is only very preliminary results that suggest a possible solution. |
Understood!
I have some basic measurements taken from Miecze Średniowieczne z X–XV Wieku by Marian Glosek, and the photo agrees very closely: L: 95; BL: 80.8; HL: 14.2; CL: 16.2; BW: 4.4; PH: 3.2; PW: 7.1 cm. Some of the predicted ratios can also be checked from this: HL/CL = 0.876, compared to √3/2 = 0.866.
The pommel seems to be bit larger than what is predicted by the hexagon and two circles anyway... A closeup of the hilt shows this a bit better.

|
|
   |
 |
J. Nicolaysen

|
 Posted: Thu 24 Nov, 2016 8:03 am Post subject: Posted: Thu 24 Nov, 2016 8:03 am Post subject: |
 |
|
If you guys aren't inscribing your doodles on vellum with compass, calipers and square, I don't think you can trust your accuracy.
http://thomasguild.blogspot.com/2013/01/the-m...liper.html
All in good fun. It's above my head anyhow. Sure appreciate the level of intelligence and precision tho.
|
|
  |
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
You cannot vote in polls in this forum
You cannot attach files in this forum
You can download files in this forum
|
All contents © Copyright 2003-2026 myArmoury.com — All rights reserved
Discussion forums powered by phpBB © The phpBB Group
Switch to the Basic Low-bandwidth Version of the forum
|

