| Author |
Message |
|
Karl Randall
|
 Posted: Fri 11 Dec, 2009 5:43 pm Post subject: Posted: Fri 11 Dec, 2009 5:43 pm Post subject: |
 |
|
| Quote: | | Optimum performance with heavy arrows, to be able to have high energy without great speed, giving excellent penetration, which perhaps even a ballista would not be ashamed of (Gerald). |
Yessss.....but it helps to understand that energy is proportionate to the SQUARE of the velocity, while only scales LINEARLY with mass.
Energy = Velocity^2 x (Mass/2)
Every bow (or gun, catapult or other means of delivery) has a "best" solution when it comes to ammunition weight. Actually, several "best" solutions, depending if you are solving for range, energy transfer or accuracy (the longer a projectile is in flight, the greater the affect gravity has on targeting, making it more difficult to achieve a given level of accuracy).
A ballista has a heavier arrow for two reasons. First, the arrow must be thick enough to undergo the energy transfer process (acceleration) without breaking. Second, a heavier arrow transfers a greater amount of energy to the target on impact.
But - and here's the rub, as an arrow increases in mass, it will gradually lose velocity. There is an optimal point where energy increases in mass are balanced out by energy losses in slower velocity. Looking back at our energy equation, an unduly heavy arrow looses energy compared to an arrow of optimum weight rather quickly, due to the squaring of velocity.
In general then, if you can get increased velocity for a small loss in mass you should do it, so long as your arrows can withstand the stress. At some point arrows start breaking though at which point you are indeed better off with a more massive missile.
Bullets are horrendously more complicated as drag suddenly increases rapidly at speeds of over 800 feet per second. Thankfully arrows don't come close to reaching this speed when launched by a bow, ballista or other mechanical means.
|
|
   |
 |
|
Timo Nieminen
|
 Posted: Fri 11 Dec, 2009 6:59 pm Post subject: Posted: Fri 11 Dec, 2009 6:59 pm Post subject: |
 |
|
| Karl Randall wrote: |
But - and here's the rub, as an arrow increases in mass, it will gradually lose velocity. There is an optimal point where energy increases in mass are balanced out by energy losses in slower velocity. Looking back at our energy equation, an unduly heavy arrow looses energy compared to an arrow of optimum weight rather quickly, due to the squaring of velocity.
In general then, if you can get increased velocity for a small loss in mass you should do it, so long as your arrows can withstand the stress. At some point arrows start breaking though at which point you are indeed better off with a more massive missile.
|
While the arrow does need to be strong enough to not break, there's more to it than that. The energy stored in the bow depends on the draw weight and draw length (and how the force required to draw the bow changes along the draw), and is independent of the mass of the arrow used.
If that was the whole story, you'd get the same energy in any arrow (of sufficient length), and lighter arrows would be better every time.
However, some of the energy stored in the bow goes into moving the limbs. As the arrow becomes lighter, more and more of the energy goes into moving the limbs, and less into the arrow. So, the lighter arrow has less energy. It will still have more speed - more energy going into the limbs of the bow means that the limbs are moving faster, and the arrow also moves faster.
Conversely, the heavier the arrow, the more energy it gets, but the slower it moves. Yes, it's slower due to the higher mass, but it will have more energy.
Penetration depends on energy, range and accuracy depend on speed. Which do you prefer? Of course, some compromise will be best, but exactly where one compromises depends on what one wants.
It isn't just the arrow that matters; it affects the design of the bow too. If you want to maximise energy, you need draw weight, even at the cost of much heavier and slower limbs. If you want speed, you want the lightest limbs for a given draw weight. This is complicated - it depends on the distribution of mass in the limbs, and more.
If an arrow is made lighter and lighter (let us assume a magic unbreakable arrow), you'll run into problems with drag eventually. The drag coefficient D will be largely independent of the mass of the arrow. The drag force on an arrow will be Dv^2, proportional to the square of the speed. Energy lost over a distance d will be dDv^2. So, a lighter arrow, with a higher speed, will lose more energy but have less energy to start with. Eventually, in theory, this will affect range. This experiment can be done by throwing ping-pong balls, squash balls, golf balls, etc. I don't expect this to be an issue in war archery with traditional bows and arrows.
|
|
   |
 |
|
Karl Randall
|
 Posted: Sat 12 Dec, 2009 5:41 pm Post subject: Posted: Sat 12 Dec, 2009 5:41 pm Post subject: |
 |
|
I certainly agree that there is more to the situation.
A longer draw length allows for more time for the arrow to accelerate and, certeris parabus, more energy will be imparted to the arrow.
I do have a genuine question however - it was my belief that the amount of energy used in moving bow limbs (and string weight while we're at it) remained pretty much independent of arrow weight.
Hence, if you have a bow with heavy limbs it will shoot arrows slower than a bow with fast limbs - for all arrow weights. I get the impression that you are saying a bow with heavy limbs will impart more energy to a heavier arrow. I'm pretty sure that just isn't the case. Heavier limbs just means a less efficient transfer of energy storage in the bow - because more of the bow itself has to move.
I am pretty sure that what you are describing is a case wherein increasing arrow mass has a negligible negative effect on velocity. This can be seen in both arrows and catapults. Essentially, you are below the optimal point in the mass/velocity equation. Obviously, with a very low weight arrow, the limbs can perhaps accelerate a bit faster than with a very high weight arrow, but the degree of change in limb acceleration is very small unless we are dealing with LARGE changes in arrow weight.
|
|
   |
 |
|
Timo Nieminen
|
 Posted: Sat 12 Dec, 2009 7:10 pm Post subject: Posted: Sat 12 Dec, 2009 7:10 pm Post subject: |
 |
|
| Karl Randall wrote: |
I do have a genuine question however - it was my belief that the amount of energy used in moving bow limbs (and string weight while we're at it) remained pretty much independent of arrow weight.
Hence, if you have a bow with heavy limbs it will shoot arrows slower than a bow with fast limbs - for all arrow weights. I get the impression that you are saying a bow with heavy limbs will impart more energy to a heavier arrow. I'm pretty sure that just isn't the case. Heavier limbs just means a less efficient transfer of energy storage in the bow - because more of the bow itself has to move.
|
Heavier limbs means slower arrows, for all arrow weights, as long as the draw weight of the bow is the same. With similar construction, heavier limbs usually result in higher draw weight. You don't ever want heavier limbs, but sometimes you accept them.
| Karl Randall wrote: |
I am pretty sure that what you are describing is a case wherein increasing arrow mass has a negligible negative effect on velocity. This can be seen in both arrows and catapults. Essentially, you are below the optimal point in the mass/velocity equation. Obviously, with a very low weight arrow, the limbs can perhaps accelerate a bit faster than with a very high weight arrow, but the degree of change in limb acceleration is very small unless we are dealing with LARGE changes in arrow weight. |
To shoot a lighter arrow, say, 10% faster, the limbs need to move 10% faster. The bow then wastes 21% more of the total available energy. Since the total energy is still only the same, the arrow must end up with less energy. The lighter arrow is always shot faster, but with less energy. A heavier arrow always has more energy, but less speed.
There is a particular weight of arrow that is important (for a given bow), but I don't know if it can be properly described as "optimum", and it means that changes in arrow weight are important for both energy and speed. OK, here goes, with plenty of approximations for simplicity. Consider shooting an arrow of mass m at speed v.
The limb will move (in some average sense) at some speed V = fv that is some fraction f of the arrow speed v. How large is f? The tip of the limb will move at approximately v/2, the centre of mass of the limb at less than half of this again. So, we should have f < 0.25. Perhaps f = 0.1 might be a good estimate?
For a draw weight of F increases linearly from zero over a draw length L, the total energy stored in FL/2, whic provides the energy of the bow and arrow, so
FL/2 = (1/2) (mv^2 + MV^2)
or
FL = (m + f^2 M)v^2
for limbs of mass M. From this, easy to calculate the speed of the arrow. The energy of the arrow will be
(1/2) mv^2 = (1/2) m FL/(m + f^2 M) = (1/2) FL/(1 + f^2 M/m).
Once m becomes much smaller than f^2 M, the energy goes down quickly for only small gains in speed. Conversely, if m becomes much larger than f^2 M, the speed drops very quickly for only a small gain in energy. So you want m to about f^2 M. But with m in this range, you see reasonably large changes in both speed and energy, so exactly what arrow weight you want depends on what you want to do with it. Carry 2 kinds of arrows. Lighter arrows with lighter heads for longer range, heavier arrows for shorter range penetration. If you didn't get a significant change in performance, why would anybody have bothered to carry different kinds of arrows?
It affects bow design too. If your arrows need to be at least of some particular weight in order to survive shooting, there will be some limb weight after which relatively little is gained by further lightening.
[/b]
|
|
   |
 |
Dan Howard

|
 Posted: Sat 12 Dec, 2009 10:27 pm Post subject: Posted: Sat 12 Dec, 2009 10:27 pm Post subject: |
 |
|
| Timo Nieminen wrote: | | Why do you think it's wrong? |
A more accurate translation of Gerald's latin would be
"...bows made of wild elm, unpolished, rude and uncouth, not only calculated to shoot an arrow to a great distance, but also to inflict very severe wounds in a close fight"
|
|
  |
 |
|
Karl Randall
|
 Posted: Sat 12 Dec, 2009 10:45 pm Post subject: Posted: Sat 12 Dec, 2009 10:45 pm Post subject: |
 |
|
| Quote: | | The lighter arrow is always shot faster, but with less energy. A heavier arrow always has more energy, but less speed. |
I am going to conditionally agree with this statement.
If what you are describing is depicted as a force graph, it would look like an outward shift in entire force/draw curve (since it would necessitate changing to a higher draw weight. If you wanted to keep the same draw weight then you could change from say a longbow to a highly reflexed composite or even a compound bow: both would start at the same point, but the compound bow would have a force/draw curve that would bulge more, representing a greater amount of stored energy.
Then you could shoot all arrows faster as compared to the longbow. It would also likely have an arrow of a greater weight if solving for optimized energy. But again, if you continue to increase arrow weight beyond that optimum point, small decreases in velocity would not be made up by increased arrow weight.
In other words, increasing energy storage/efficiency of the bow leads to an new optimal energy solution, but there still is an optimal point.
All I am saying is that there IS an optimum energy balance between ammunition weight and velocity. This point is not the optimum point for range, or accuracy, or "stopping power" (which is potentially starting to digress into the realm of firearms). But continued increases in arrow weight beyond that optimal point and you get a total decrease in energy, rather than continued increases.
|
|
   |
 |
|
Timo Nieminen
|
 Posted: Sun 13 Dec, 2009 12:31 am Post subject: Posted: Sun 13 Dec, 2009 12:31 am Post subject: |
 |
|
| Karl Randall wrote: | | Quote: | | The lighter arrow is always shot faster, but with less energy. A heavier arrow always has more energy, but less speed. |
I am going to conditionally agree with this statement.
If what you are describing is depicted as a force graph, it would look like an outward shift in entire force/draw curve (since it would necessitate changing to a higher draw weight. If you wanted to keep the same draw weight then you could change from say a longbow to a highly reflexed composite or even a compound bow: both would start at the same point, but the compound bow would have a force/draw curve that would bulge more, representing a greater amount of stored energy.
Then you could shoot all arrows faster as compared to the longbow. It would also likely have an arrow of a greater weight if solving for optimized energy. But again, if you continue to increase arrow weight beyond that optimum point, small decreases in velocity would not be made up by increased arrow weight.
In other words, increasing energy storage/efficiency of the bow leads to an new optimal energy solution, but there still is an optimal point.
All I am saying is that there IS an optimum energy balance between ammunition weight and velocity. This point is not the optimum point for range, or accuracy, or "stopping power" (which is potentially starting to digress into the realm of firearms). But continued increases in arrow weight beyond that optimal point and you get a total decrease in energy, rather than continued increases. |
There certainly is an optimum arrow weight, for a given bow, and for a given purpose. But it doesn't provide optimum velocity, or optimum energy, or any optimum single[i] thing. Rather, optimum [i]performance, which is a composite of many single factors.
I must disagree with your last sentence. The heavier arrow will always have more energy. It's shot slower, so the bow moves slower, and so the bow gets less of the total energy. What you will get a decrease in is performance. And that's the important thing. Energy, by itself, doesn't matter. Speed by itself doesn't matter. Energy in the arrow is useless if it cannot be delivered to the target. This takes speed. Hitting the target with negligible effect is useless; that takes energy. What is important is that, after some weight, any increased arrow won't result in a large enough increase in energy for the decrease in speed to be worthwhile, or perhaps even the increase in weight you need to carry in order to carry the arrows. Given that there is only a finite amount of energy stored in the bow, all you can do is approach that value - you're not going to get any more energy than that. Once you have a sufficiently large fraction of that, only a small increase will be possible. Not a worthwhile increase, but, technically, an increase.
The graphs show the increase/decrease in energy and speed. That you'll get poor performance from too heavy/light arrows is pretty clear.
That's all for the same bow. Varying the bow, you'll always gain from heavier draw weight, lighter limbs, longer draw, better draw force curve. As long as your archer can draw the bow, you can afford to buy the bow, the bow doesn't break, the bow doesn't get too large to use or carry around, etc.
Technical points about energy can be misleading about the real performance. They can make for fine deliberately misleading rhetoric. But, IMHO, it's still best to be correct on the technical points, and clarify as needed.
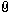 Attachment: 3.79 KB Attachment: 3.79 KB
Speed of arrow vs mass of arrow
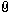 Attachment: 4.16 KB Attachment: 4.16 KB
Energy of arrow vs mass of arrow
|
|
   |
 |
|
Karl Randall
|
 Posted: Sun 13 Dec, 2009 3:19 am Post subject: Posted: Sun 13 Dec, 2009 3:19 am Post subject: |
 |
|
OK...I am preparing to stand corrected.
First, however I am quite interested in your graphs. Were did the data for them (or completed graphs)?
The first graph in particular looks right. I am unsure I understand the units and scale used however. It looks like velocity doesn't change much at all, while arrows mass ranges to the extreme. I presume that the scaling was done in a program and you couldn't get it to label the axes quite the way you liked? I have exactly the same problem with excel, to the point that I actually gave up trying to use it for making graphs. No matter, the first graph is most certainly shaped correctly, which is what we are really after.
The second graph however appears odd to me. Did you use the data from the first graph to generate the second graph? Can you overlay velocity so that can also be shown? I will also admit to the possibility that the second graph looks odd because it is going counter to my expectations, which, while I'm pretty sure are sound, I have yet to test myself.
Logically however, if you continue to increase arrow weight ad absurdium, you wind up trying to launch saplings. Let's assume one will go a few meters - will a sapling going an extremely short distance have more energy than a properly-adjusted arrow? My brain is telling me no, but then my brain is also looking at your second graph and realizes that I have not done a data chart for myself.
|
|
   |
 |
M. Eversberg II

|
 Posted: Sun 13 Dec, 2009 6:12 am Post subject: Posted: Sun 13 Dec, 2009 6:12 am Post subject: |
 |
|
Wouldn't a "lighter arrow" at some point impart more force than a heavier one? F=MA; if M is the same and A increases, eventually F will be higher wouldn't it?
Mind, I'm terrible at this stuff.
M.
This space for rent or lease.
|
|
      |
 |
|
Timo Nieminen
|
 Posted: Sun 13 Dec, 2009 11:34 am Post subject: Posted: Sun 13 Dec, 2009 11:34 am Post subject: |
 |
|
| Karl Randall wrote: |
The second graph however appears odd to me. Did you use the data from the first graph to generate the second graph? Can you overlay velocity so that can also be shown? I will also admit to the possibility that the second graph looks odd because it is going counter to my expectations, which, while I'm pretty sure are sound, I have yet to test myself.
Logically however, if you continue to increase arrow weight ad absurdium, you wind up trying to launch saplings. Let's assume one will go a few meters - will a sapling going an extremely short distance have more energy than a properly-adjusted arrow? My brain is telling me no, but then my brain is also looking at your second graph and realizes that I have not done a data chart for myself. |
The graphs are just my previously posted equations. The 2nd is generated from the 1st, but it could be done the other way too. The automatic labelling of the horizontal (logarithmic) scale would have been in scientific notation, so I converted that to 1/1000, etc. Here is a combined graph.
The upper limit to the arrow speed is due to the upper limit to the speed the bow can moves its own limbs, even without an arrow (or with an arrow of zero mass).
The energy result is less intuitive. I think of it as a consequence of the bow moving ever more slowly with heavier arrows - the original energy is there, but less and less goes into the limbs. It has to go somewhere, and that somewhere is the arrow.
But once the arrow is heavy, the gain is only small.
The 2nd graph can also be misleading about the effect. Penetration depends on more than just the energy; the target will be moved by, rather than damaged by, a sufficiently slow and heavy projectile.
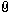 Attachment: 12.62 KB Attachment: 12.62 KB
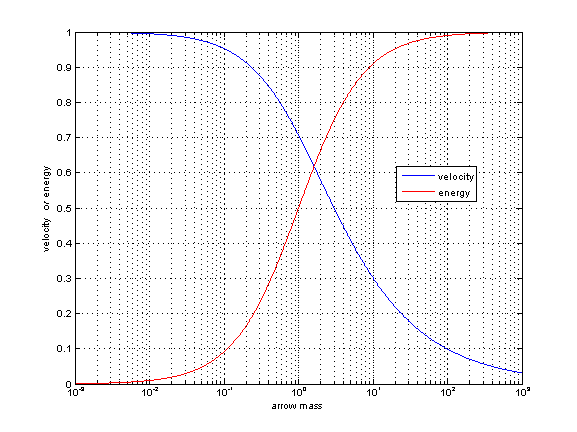
Combined graph of arrow velocity and energy.
|
|
   |
 |
|
Timo Nieminen
|
 Posted: Sun 13 Dec, 2009 12:16 pm Post subject: Posted: Sun 13 Dec, 2009 12:16 pm Post subject: |
 |
|
| M. Eversberg II wrote: | | Wouldn't a "lighter arrow" at some point impart more force than a heavier one? F=MA; if M is the same and A increases, eventually F will be higher wouldn't it? |
Sure! (But note that "if M is the same", the arrow isn't lighter!)
Translating that F into what happens to the target is not so simple - the time over which the force applied matters very much. For similar projectiles (e.g., arrows with similar heads) hitting at not too dissimilar speeds, the useful number is the energy. For the classic case of shooting ball-bearings into clay, the distance of penetration into the clay is proportional to the energy. This will still hold for a range of ball-bearings of different masses as long as they're the same size (make them of different metals, hollow, or such). IIRC, the original motivation of many such early experiments was naval gunnery and its effect - the penetration of cannonballs into wood.
There's a common case of faster lighter arrow exerting more force than heavier ones - air resistance. Take two arrows of different weights, same size, at the same speed. The air resistance on both is the same, so the light one slows down faster. From your F=MA above, same F, less M, higher A. Now, if they have the same energy, the lighter one is moving faster. The drag force on the lighter arrow will be greater, since it's proportional to v^2. The rate at which energy is lost is proportional to F times speed, so is proportional to v^3. Light arrow loses energy faster, so, after being shot at the same energy, it has less energy than the heavier one.
At some point, a lighter arrow means less range! (Try throwing beach balls vs basketballs and see for yourself.) At lower speeds, you're mainly worrying about gravity, and more speed is better. So, there will be some arrow weight that will give maximum range. But if you're worrying about that, you'll modify the arrow in more ways than the mass - try and change the drag too. E.g., http://www.second-opinions.co.uk/flight-arrows.html, especially the parts about drag and fletching.
|
|
   |
 |
M. Eversberg II

|
 Posted: Sun 13 Dec, 2009 6:17 pm Post subject: Posted: Sun 13 Dec, 2009 6:17 pm Post subject: |
 |
|
Good point on the M changing; it made sense at the time.
I'm not terribly good at head math.
M.
This space for rent or lease.
|
|
      |
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
You cannot vote in polls in this forum
You cannot attach files in this forum
You can download files in this forum
|
All contents © Copyright 2003-2025 myArmoury.com — All rights reserved
Discussion forums powered by phpBB © The phpBB Group
Switch to the Basic Low-bandwidth Version of the forum
|

