Wow. this is some awesome stuff, and it being made a spotlight topic is awesome.:eek: :) :D :lol: One thing I should have said in my original post is that, though I now know of the existence of vibration nodes, I’m not even really sure exactly what they are. :wtf: :?:

Hi Chaps,

They really shouldn't have threads like this - my head is *still* hurting trying to take it all in...:-)

But seriously guys - this has to be one of the most fascinating and informative threads I've read in a while - it just shows that there is *always* heaps more to learn about our hobby...

Peter - I'm eagerly awaiting my Albion Swords Solingen sword - that and the Saint Maurice are going to be my first two reproduction/recreation Mediaeval swords I think...

This discussion has helped me *enormously* to get a bit more of an understanding of the complexities/interrelationships when it comes to the dynamics of the Mediaeval sword. I had *no* idea there was so much to it - nor any idea that our ancestors of 700 or 800 years ago were so advanced in terms of their maths and physics (although they would have never used these words).

Anyway - enough waffle from me - please continue - I'll be quite honest and say right now I'm going to have to read this thread 3 or 4 times before everything sinks in...

Actually: I will 'throw in' one quick question to you all - given the complexities/intricacies of what you've been discussing do you think that our European swordsmith ancestors of, say, the 13th century, actually worked to specific FORMULAE of some sort? (formulae only available to those initiated into the guild or whatever and subsequently lost to time) OR, do you feel that most of this was simply a matter of some sort of 'evolution' achieved through trial and error... (or both?)

John.

Hello Guys

Good stuff all around here. I may be able to play with Vincent's numbers a bit tomorrow on some of the originals and will report back. Also Vincent thank you for posting the source for the diagram I had meant to add it to the post and forgot by the time I finished writing, For anyone how missed it good site to get some basics is HyperPhysics site

Peter as far as rotational points I can give you my take on where I am at with these. Gus and I have talked about this a while ago and I am unsure of exactly where he was at with them so this should be seen as my own personal take and not referenced to any other use of the term.

In use I started to see some elements that you described in your discussion of the pivot points and the effect this had on a practical use of the sword in play that was at least attempting to be based on the period movements we are interpreting from the manuals. The result was I started to work on the concept of a rotational point; I call this the "Active Rotational Point" of the sword. Sadly this is a fuzzy thing. It will change for each piece and for different actions with the same piece but it is the point where the sword wants to move around in play. The dynamic of this is that there is a point with any given action of the sword that the piece will want to rotate or strike around in action. This in some cases will be the moment of inertia. In other cases it seems to be the "quite" spot in the movement of the body and sword as a complex unit. Does that make sense?

In the case of a falling cut from say vomtag with minimal elbow and wrist action the moment of inertia will be the joint of the shoulder. In the case of the movement of the hand and lower arm in a crossing motion across the body while still keeping the opponent on point you will have a rotational point out mid blade. If you have a rapier and you are keeping the opponent on point but moving the guard into different quadrants to control lines you will be rotating the piece about a point some where near or even beyond the tip. These are all points that will adjust to sword action, grip style, arm action, body motion and our list of sword attributes. This, in a way, is almost a way of thinking about the combat as much as a physical attribute of the sword.

Now the difficulty in measuring and defining this point is significant for the very reasons stated above and my fuzzy brain has probably clouded the issue more than clarified but this is an important working attribute of the weapon in play to me and one that I think is a component of what fencers will call "feel" when they are describing the sword they would like.

Best
Craig

Hello all,

I've tried to make an illustration for pivot points and their geometrical meaning, and here is what I ended up with...

I've based the drawing on the Talhoffer, but it should be taken with a grain of salt since I don't have a really good idea of where its pivot points are... So it's mainly an illustration of the geometrical construction.

So here you have what Peter Johnsson calls forward pivot point (P2), aft pivot point (P1), and the center of gravity G. I've added a third couple of reference/pivot point H3, P3 to illustrate the geometrical construction.

Here goes the explanation:

Let's say that we know that the pivot point associated with the cross (in H2) is P2. I've drawn it close to the tip, based on an earlier post from Peter Johnsson ("Pointy longswords will by nature therefore have a forward pivot point close to the point (at the point or a short distance behind it)..."). These two points define a segment upon which you can build a circle with diameter H2P2.

Now if you raise from G the perpendicular to the axis of the sword, it intersects the said circle at point O (like, origin since it plays a central role in the following). Note that by construction, the triangle H2 O P2 is a right triangle.

And here is the interesting bit: for any reference and pivot point H and P, this holds true, the triangle H O P is always a right triangle. I can give the mathematical demonstration of this if anyone is interested, it proceeds from the relation I wrote in my answer to Greyson.

Anyway, finding other pivot points is now easy, because it only involves building a right triangle. So for example to find the aft pivot point P1, I draw the line H1 O, and then an orthogonal line from O that intersects the axis of the weapon in P1. Same goes for any reference point... For example I've drawn the pivot point associated to the riser, here P3. I've given a different color to each of these triangles to make them stand out better.

Each distance in this diagram has a physical meaning. For example, the square of the distance OG, multiplied by the mass of the weapon, is the moment of inertia of the weapon, i.e. it measures how difficult it is to get it to rotate around G. Similarly, the square of the distance 0H1 gives the moment of inertia around H1, so that would be how difficult it is to rotate around H1... If you just use torque, that is.

And finally, you could put several weapons on the same diagram, placing them such that they share the same origin O (it's simply a matter of moving their center of gravity vertically). And then you are able to visualize simultaneously the lengths, the center of gravity, the inertia, and the pivot points, by rotating a right triangle around O. Every dynamic and geometrical properties just in one drawing...

Sadly, as far as I can figure out, the harmonic nodes cannot be represented by such simple means. So I have left them out of this...

There are other observations you can make with that. For example, note how the distance between H1 and P1 is almost the same as the distance between H3 and P3, but greatly less than the distance between H2 and P2. This means that pendulum-like motions around H1 and H3 (for example, during cutting) share some properties in speed of realignment with the motion of your arm. It would be a totally different story from H2... You could also note how the tip control properties vary greatly with just a small modification of H2... And I could go on and on :)

I hope this can help clarifying some of the complexities...

---

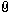 Attachment: 18.46 KB

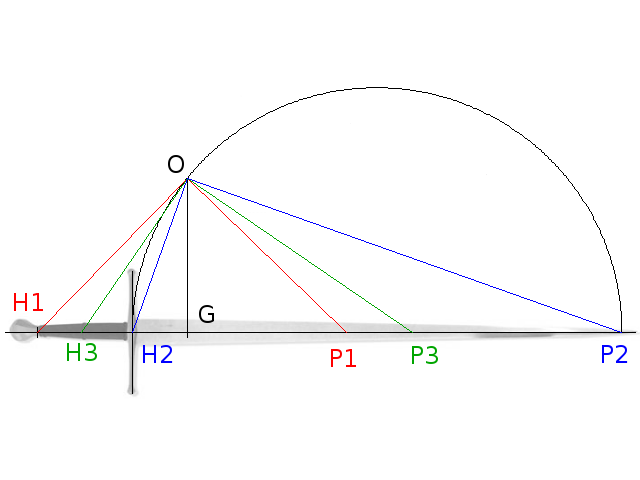
An illustration of the geometrical properties of pivot points

Taylor,

I agree with what you are saying. In almost all (maybe all?) WMA’s, we’re recreating a dead art; so how are we to properly recreate the art without properly recreated tools? The emphasis should be placed on making the sword as historically accurate as possible. Then our art should adjust itself to the use of the well made weapon.

However, it really is a misconception that katana are light weight. They usually weigh about same as a longsword and have quite thick spines with significant blade presence. Deep cutters indeed. Some katana are built with thinner blades and less weight for the practice of iaido, but these are not accurate of what would have been taken into battle.

Hey Travis,
You are right about the kat weights, but I was talking more of the handling properties. Shoulda worded it better. :)

Just thinking more about this topic… Studying the antique weaponry is really just as important as studying the fight books. These really are the only direct links to the history we study.

Which leaves an important question open: how do we study antiques ? I'd be especially interested in this with respect to martial art weapons, indeed...

You could have a purely geometrical approach, measuring every single length on the antique, and try to reproduce that exactly. I'd imagine that it's almost impossible technically. Plus, if you don't use the exact same materials, you can still end up with an unbalanced weapon. I think everyone here agrees that there is more to it than just geometry... Reproducing materials with enough precision would be extremely difficult, not to mention measuring the properties of the materials on the antiques in the first place (remember that for proper balance you'd be interested in the inside of the weapon as well, which would probably mean destroy it while trying to reproduce it. Not a good deal at all :eek: ). As far as I know, all the makers try to copy not just the geometry and materials, but the balance as well.

In order to adjust balance there are two attitudes I can think of. You can just trust your feeling, or you could try to measure the balance.

The first case can be very successful indeed. But it's not something anyone else can re-use, since there is nothing measured. It's purely personal and subjective. You have no mean to describe what you were adjusting. That, and different individuals could be sensitive to different effects of dynamic properties. Though it feels the same to you, it does not necessarily means it feels the same to me. And it could require having access to the antique weapon during the whole process, in order to be able to compare...

As far as I'm aware, the full intuitive approach is not really used today for the making of reproduction. Mass and center of gravity are two things that are often measured, along with the center of percussion and possibly other nodes of vibration. Those properties of antiques are interesting because they allow objective comparison with the reproduction. Apparently, Peter Johnsson adds pivot points to those significant measurements of balance, an idea I strongly agree with since they are the most precise way to measure the inertia, a quantity that is important for any rotating object.



That's not to say that there should be nothing subjective left. There will always be, since perfect reproduction in every aspect is probably not possible.

One immense value I see in these threads is that they can enhance our comprehension about what is possible or important to measure on antiques. Remember that those measurements can then be transmitted to someone who hasn't been in contact with the original, or that you can keep them if you don't have an access to the original anymore. I really believe it's important to measure objectively what we can, and what is proven to be significant. Hand-on contact with antiques still is a rare thing...

Then the part about the interpretation of measurements in terms of handling properties is more debatable. I do that more from a user perspective, because often I'd like to have a more precise idea of the dynamics of a weapon for sale, than just a center of gravity and a mass. Of course there are reviews... but they are often subjective on the matter of handling anyway ;) Should the comprehension of the dynamics of weapons be limited to sword makers ? In my point of view, as users we can use this knowledge as well. At least I hope so, since I'm not becoming a swordsmith in any foreseeable future :(

Anyway I hope that through threads like this people can get a better grasp of the physics involved in swords... This could help anyone that considers a sword as a dynamic, living object. Understanding and measuring does not mar the beauty of the object, to me it had quite the opposite effect...

Regards