As a follow-up to two recent discussions, I have tried to go a bit further on the simulation of sword balance... The first discussion was raising the problem of the computation of CoP. The second discussion was one I started when I figured how dynamic properties and harmonic balance could be linked. In both of these threads the problem of simulation was raised, and working on this I got some interesting results I wanted to share.
I built a small Scilab program to simulate blade harmonics and dynamic properties (pivot points, center of gravity, mass), taking as inputs parameters from the materials (density, elasticity) and geometry (lengths and cross-sections). I chose a simple model for the sword, in fact one of the simplest models for slender, flexible beams (the name of the model is Euler-Bernoulli), that allows a varying cross-section along the length of the beam. The program solves the equation from the model using a 1D finite elements approach, and finds the modes of vibration, assuming that the sword is not constrained by anything. That's the best way, I think, to simulate the very relaxed grip that is assumed when looking for vibration nodes.
Being satisfied with the behavior on basic test cases (uniform bar, simple taper, and so on), I decided to go for something a bit less obvious and tried to simulate a real sword of mine: my Angus Trim type XI. To be honest, I was expecting a more or less spectacular failure :)
I measured as precisely as I could cross sections across the blade, as well as the pommel and cross-guard. I didn't want to go through the trouble of unmounting the sword so I made some reasonable guess for the tang based on what I remembered. I completely neglected the grip (I can hear the screams of horror already ;) )...
I ended up with 7 parts for the sword, over which I assumed the variation were linear, that I further subdivided in elements roughly according to their length:
* pommel (1 element)
* tang (5 elements)
* cross (1 element)
* upper part of the blade (30 elements)
* middle part of the blade (10 elements), the fuller stops here
* upper part of the blade (5 elements), not fullered
* tip (1 element)
I entered all this into the program, along with average values of density and Young modulus for steel, aft and forward positions on the grip (to compute aft and forward pivot points), and watched the results...
They are surprisingly good :cool: Figures and explanations follow...
In fact it gives the dynamic properties with a precision better than half a centimeter (far better than I can measure anyway). I just tweaked slightly the pommel shape to adjust even better (when I say slightly, it's 1mm in thickness...). And that is with all the approximation made, and a very rough model of the fuller... The harmonic nodes are also very precisely computed, from what I can see. The blade node is exactly right, the hilt node is a bit more difficult to measure, but seems to be spot-on as well.
I had to adjust the density slightly to account for the mass of the sword. My first simulation was giving a mass of 950g, while my sword weights 1011g. This uniform change does not moves the nodes or pivot points at all (this is a mathematical property of the model I use).
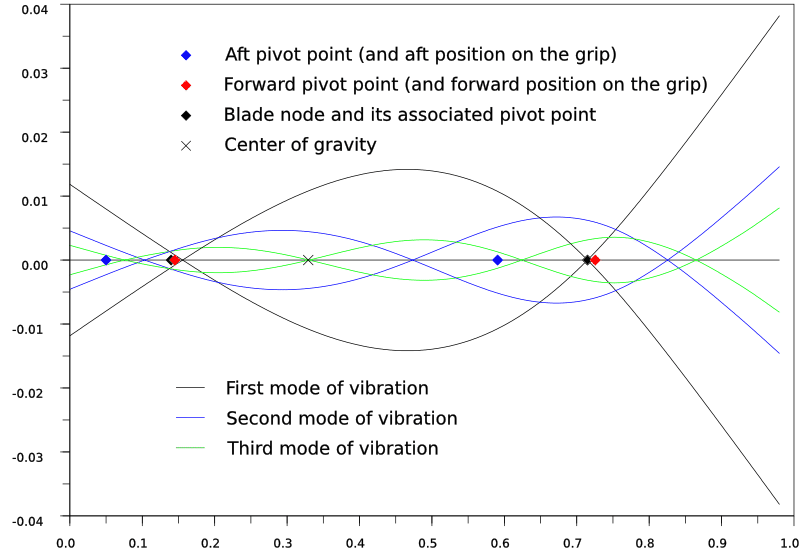
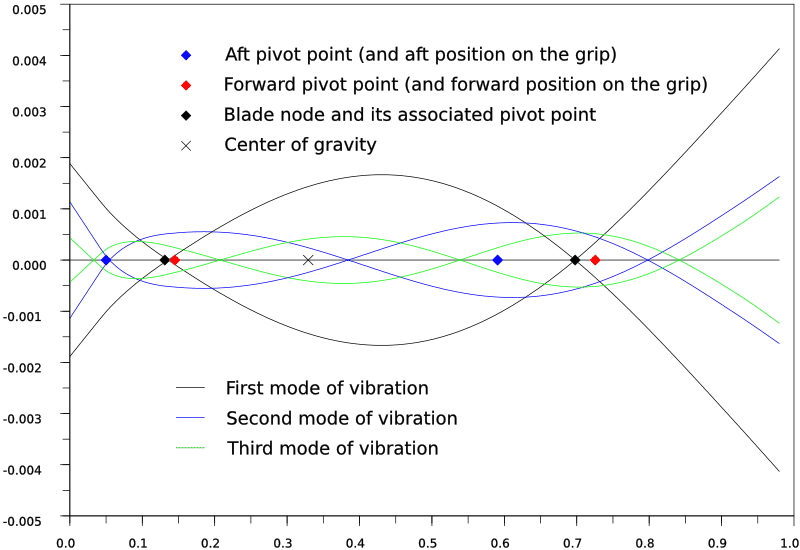
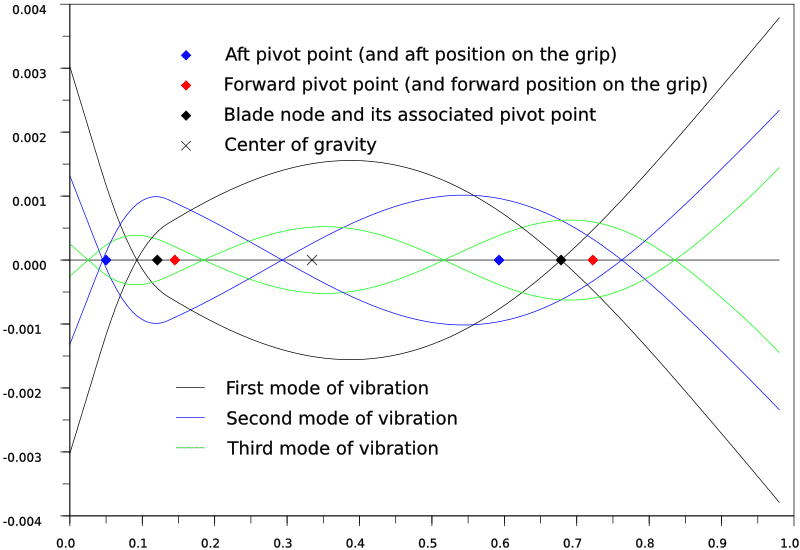
I made two figures, one with the blade alone, and the other for the full sword.
The straight black line is the axis of the undisturbed sword. The tip of the sword is to the right.
The curves represent the modes of vibration. The first mode, that is used to determine the CoP given in reviews, is in black. The curves are scaled according to the energy of the sword when it vibrates in that mode: the higher the mode, the less ample the vibration becomes. I plotted only the three first modes to keep the figure clear. For each mode, I made two symmetric curves, that indicate the deformation of the sword bending one way, then the other.
The center of gravity is marked with a black X. The aft pivot point is the blue diamond, the forward pivot point is the red one. The black diamonds are the blade node and its associated pivot point. One of my goal in doing this kind of simulation was checking how close the pivot point of the blade node was to the handle node. As you can see, they are very close indeed, less than 2cm away from each other.
On these figures appear much of the phenomenon I've heard described. Note how little the aft pivot moves between the bare and the mounted blade. This pivot point is key to the cutting motions and timing of the sword, and this shows how it depends almost on blade alone. The blade node also stays roughly at the same place between the two cases. The addition of the pommel modifies the balance by bringing the forward pivot toward the tip, the handle node toward the grip, and the center of gravity back. This diminishes the blade presence and enhances the tip feeling.
I remain convinced that the interest of such simulation is limited, because the interesting results are easily measured on swords. However, it shows what is sufficient to obtain the observed effects. It also disproves a relatively widespread idea on this matter, that it should take an army of scientists and a cluster of supercomputers to accurately model and simulate the behavior of a sword because they are somehow "infinitely complex". I must stress that I did all that using well-known mathematical methods and the simplest models, implemented in the most direct fashion, and that the core of the computation runs in about 0.1 second on my laptop (far less than what it spends plotting the results, in fact. The total is about 1s...). It proves me wrong as well, because before doing this I used to think that the number of cross sections that should be measured would have to be far greater...
Besides, the program allows for some experimentation without being a smith, which is enjoyable in its own right :) I don't know how interesting for sword makers such a program could be. I suspect not much...
I would greatly value feedback about the result, what is missing, what looks wrong... There are plenty of things I still don't quite understand about harmonic balance (for example secondary nodes), so perhaps discussion of these illustrations could clarify the matter for me and for others...
I'll also try put a cleaned up, commented Scilab code somewhere on the web if there is interest.
Kindest regards
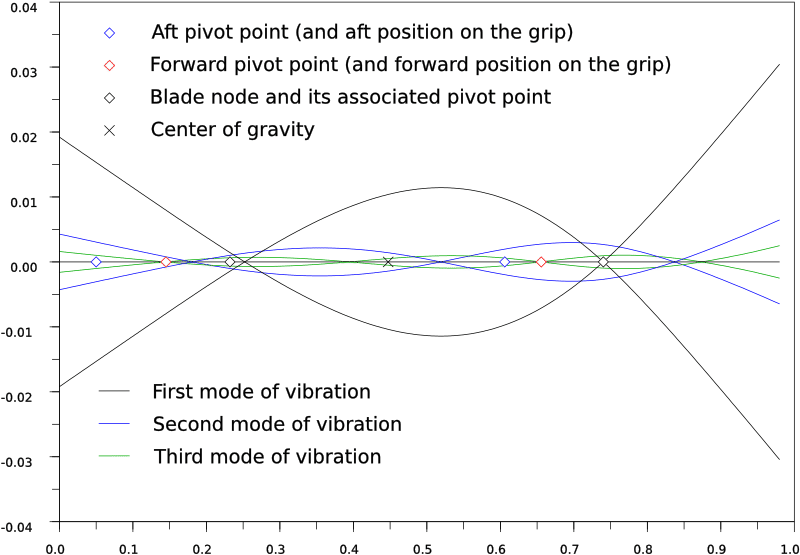
Properties of the bare blade.
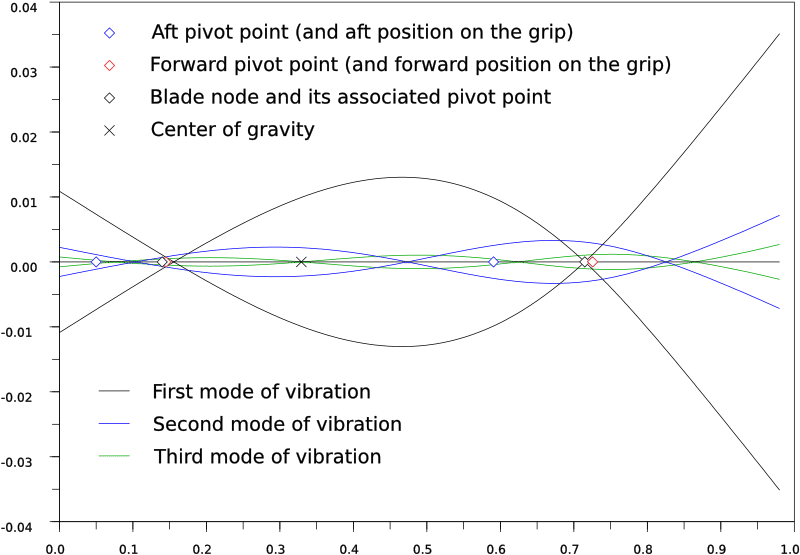
Properties of the mounted blade.